- 西華デジタルイメージ株式会社
- 技術情報一覧
- PIVとは
PIVとは
PIVとは
PIVとは、Particle Image Velocimetryの略で粒子画像流速計とも呼ばれ、空間上の粒子に対しシート状のレーザー光を短時間の間に2回連続で照射し、照射と同じタイミングで撮影された連続する2枚の粒子群画像を解析することで、2次元平面のみならず3次元情報や時系列データを取得することも可能な、方向と速度を計測する流体の可視化手法です。様々な流体力学的研究において広く使用されています。
PIVの基本原理
PIVは空間上の粒子に対しシート状のレーザー光を短時間の間に2回連続で照射し、照射と同じタイミングで撮影された連続する2枚の粒子群画像を解析することで、2次元平面のみならず3次元情報や時系列データを取得することも可能な、方向と速度を計測する流体の可視化手法です。様々な流体力学的研究において広く使用されています。
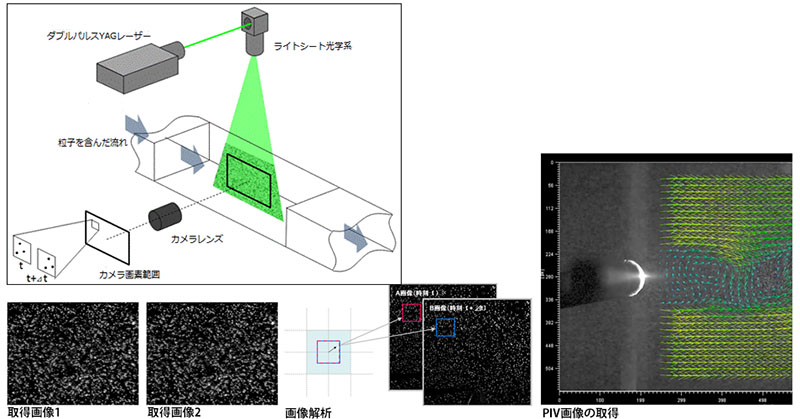
基本原理は、まず測定すべき流れを視覚化するために、小さな粒子を散布します(シーディング)。この時に形成された流れ場内の測定領域に対して、ダブルパルスYAGレーザーなどのレーザー光源を、シート状に生成する専用の光学系を通じて、シート光として照射します。そして、照射タイミングに合わせてダブルシャッターカメラで2枚連続で画像を取得します。 ダブルパルスレーザーとダブルシャッターカメラは、非常に短い時間間隔、例えば100μ秒未満の2つの粒子画像を記録するように同期されます。解析ソフトでは、取得された画像内の個々の粒子を識別することで、移動量と移動速度の両方を算出します。
レーザーライトシートに照射された面内の2次元速度成分を計測する2D-PIVや、ライトシート面内の同時多点3次元計測を実現した3D-PIV、数キロヘルツから数10キロヘルツの高速サンプリングを可能にした時系列PIV、マイクロフルイディクス流速分布解析の3D解析を可能にした共焦点マイクロPIV、BOXの中に2台のカメラを設置し、レーザーをファイバーで伝送する事により、レーザー、カメラが一体となったキャリブレーション不要のプローブ型PIV、気泡の流動をシャドウグラフ法(影絵)により撮影しPIV解析をする事で流動状況の把握が可能としたシャドウグラフPIVなど様々なソリューションがあります。ここでは、PIVの原理とPIV解析のアルゴリスム、ポスト処理について詳しく解説いたします。
PIV解析の大まかな流れ
シーディング
PIV計測を行う際に計測エリアに応じて適切な粒径のトレーサー粒子を選択して流すことは、計測精度を決定する大切な要因です。また風洞や試験体の汚染や健康被害なども考慮し、適切なシーディングを行う必要があります。シーディングについて詳しくはこちらをご覧ください。
画像の取得
PIV解析を実行するには、流れ場に対してレーザー光を2回照射して、カメラで撮影することで粒子画像を取得します。CCDやCMOSカメラの技術が進化しており、高速かつ低ノイズな画像を取得できるため、解析制度が向上しています。
フレームストラドリング
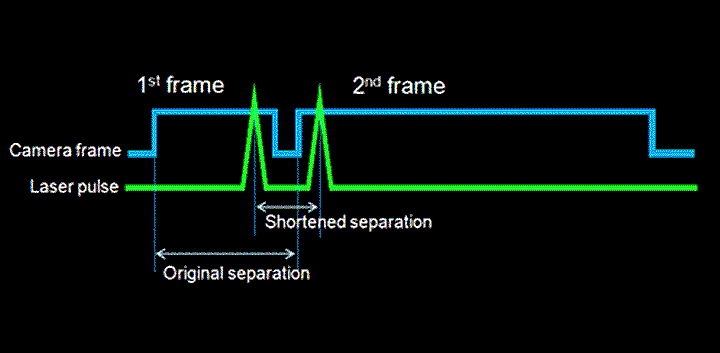
PIVは、一般的に100マイクロ秒未満の非常に短い時間間隔の連続する2つの粒子画像を必要とします。上の青い線は、2つのカメラ露光があることを示し、下の緑の線は、2つのレーザーパルスがあることを示しています。このレーザーパルスは2つのカメラ露光間のフレーム間時間をまたいでおり、このことをフレームストラドリング("frame-straddling.")と呼びます。
フレームストラドリングの手法は、100ナノ秒までの時間間隔の連続する2つの画像を記録することを可能にします。 ダブルパルスレーザーとダブルシャッターカメラは、タイミングコントローラによって同期されます。 ダブルパルスレーザは、独立して動作することができる2つのレーザヘッドを有するので、ダブルシャッターカメラの2つのフレーム間の非露光時間の長さに関わらず、ごく短時間のレーザー発振が可能です。
光学系

出力の高いレーザーを安全に用いるため、一般的には532nm付近、緑色光で用います。照射するレーザーを流れ場に導くためには、ファイバーやアームを用います。流れ場まで導かれたレーザーはシート光学系を用いて照射の厚みを調整します。シートに照射された部分の粒子画像をもって解析を行うため、シート厚の調整は非常に重要です。
また、近年ではレーザーの代わりに簡易的な測定にはLED光源も用いられますが、この場合もLED素子の指向性に合わせたシート光学系が必要になります。
適切な厚みはテスト領域によって最適なものを選択する必要があり、またカメラ側のレンズの組み合わせも解析精度を決定する重要な要素です。
解析
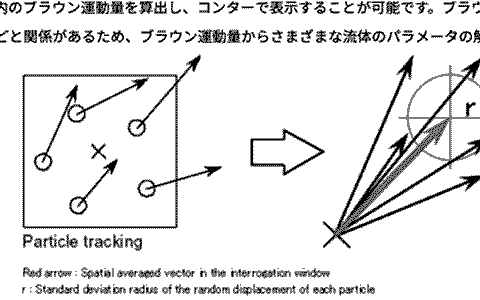
取得した粒子画像を基に解析を行い軌跡や流速を計算します。粒子の一つ一つを特定した上で解析する技術はPTV (Particle Tracking Velocimetry)と呼ばれます。PIVでは粒子画像を検索エリアで分割した上で解析を行います。
移動量と速度の評価
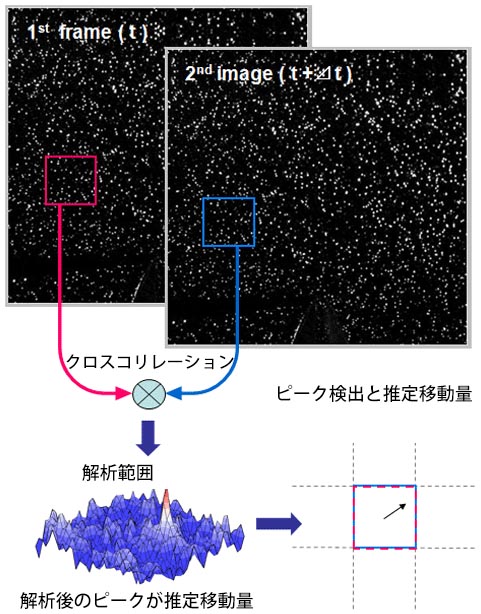
フレームストラドリングによって、PIVに適正な画像を取得すると、次のステップはPIV解析になります。 画像は小さな検索エリア、通常は32×32ピクセルに分割されます。(検索エリアは粒子画像に応じて検討します) これらの小さな検索エリアは、解析窓(Interrogation Window)と呼ばれます。
相互相関は、2つの画像の両方についてこれらの解析窓に適用され、各解析窓について相関面を得ます。 両方の画像における解析窓の位置は同じです(標準FFT相互相関では、解析窓は高度アルゴリズムによってシフトされます)。
次いで、ピーク検出および移動量評価を適用(FFT相互相関)して、ピーク検出および変位評価を適応し、各解析窓内で支配的な移動量を得ます。事前にキャリブレーションを行うことで、 フロー中(取得した画像)のピクセルのサイズおよび2つの画像間の時間間隔は判明しているので、速度を計算することができます。 取得画像におけるピクセルのサイズは、スケールを撮影し、その値を入力するなど比較的単純な較正によって決定されます。(1ピクセルあたりの距離は、スケールやターゲットを使用して実施します)
解析アルゴリズムについては、対象となる被写体のスケールや周波数によって最適となるように設計されています。
解析アルゴリズム
標準FFT相互相関
基本的な変位(速度)評価法。 短い計算時間で直接相互相関とほぼ同じ結果が得られます。
単純相関 Standard Single-Pass Interrogation
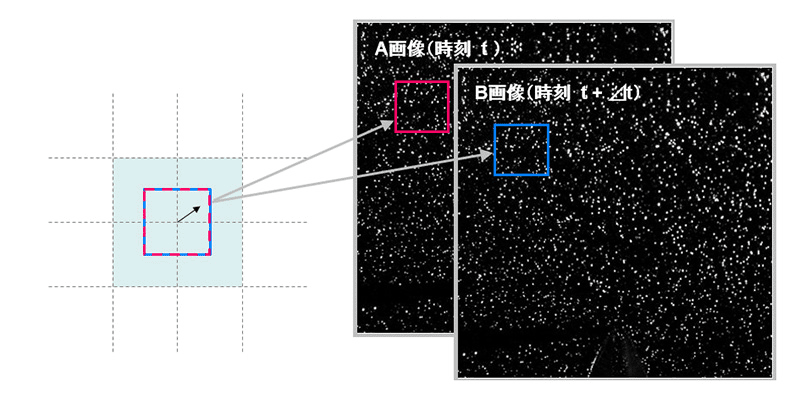
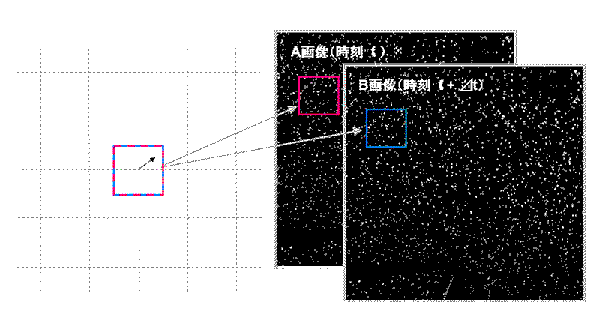
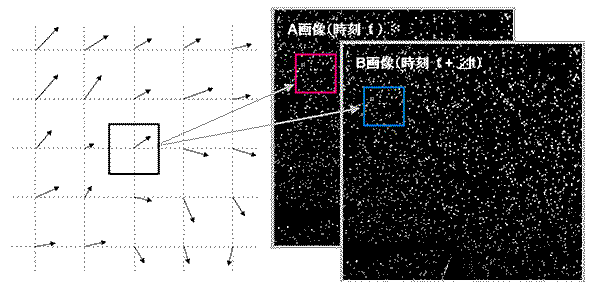
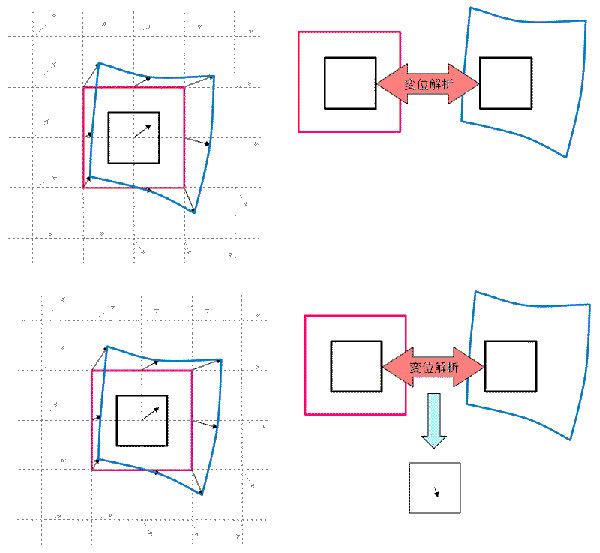
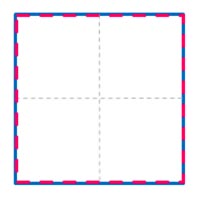
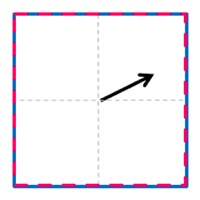
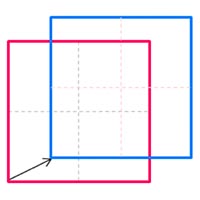
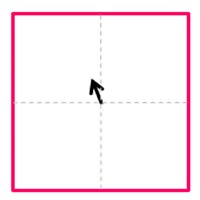
図は単純相関の概念図です。A、B2枚の画像の同一エリア(インターロゲーションウィンドウ : 解析窓)内の粒子群の移動量を相互相関解析により求めます。
再帰相関 Multipul-Pass Interrogation
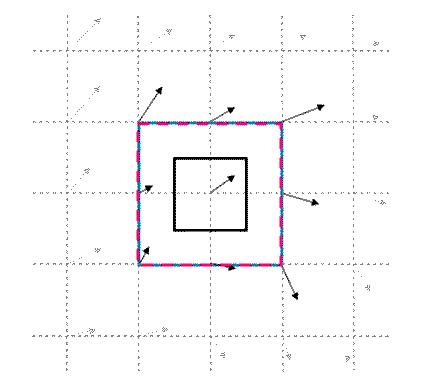
下図は再帰相関の概念図です。まず、単純相関法で得られたAB画像の相関ピークをもとに、2枚目の画像内のウィンドウを移動して、再度解析を行うことで相関値が高くなる。この操作を何度か繰り返すことで移動量が0に近づいていき、解析精度が向上します。
←横スクロールでご覧いただけます→
 |
 |
 |
 |
 |
 |
 |
| STEP1 | STEP2 | STEP3 | STEP4 | STEP5 | STEP6 | STEP7 |
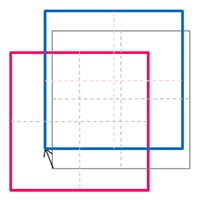
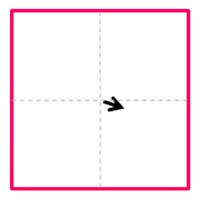
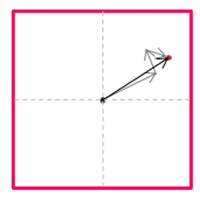
| A画像内のウインドウa(赤枠)とB画像内のウインドウb(青枠)を定義する | ウィンドウaとウィンドウbの相関をとり、移動量を求めプレディクター1とする | プレディクター1によりB画像内のウィンドウbをシフトし、ウィンドウb’とする。 | ウィンドウaとウィンドウb’の相関をとり、移動量を求めプレディクター2とする。 | プレディクター2によりウィンドウb’を再度シフトしウィンドウb”とする。 | ウィンドウaとウィンドウbの相関をとり、移動量を求めプレディクター3とする。 | この処理を繰り返すことでウィンドウ内の非対応粒子が減少し相関値が上がり精度が向上する。最終プレディクターの終点をイニシャルグリッドにおける代表移動量とする。 |
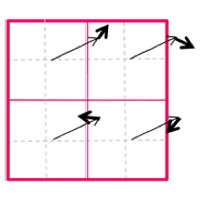
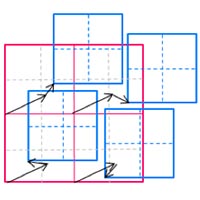
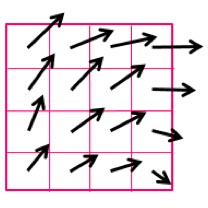
階層相関 Multi-grid Interrogation
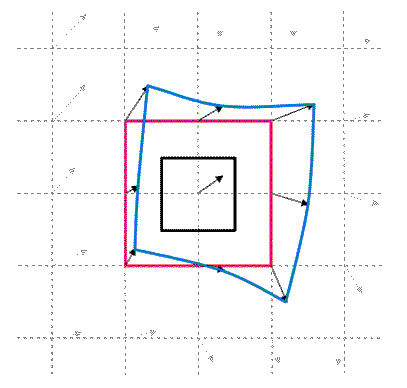
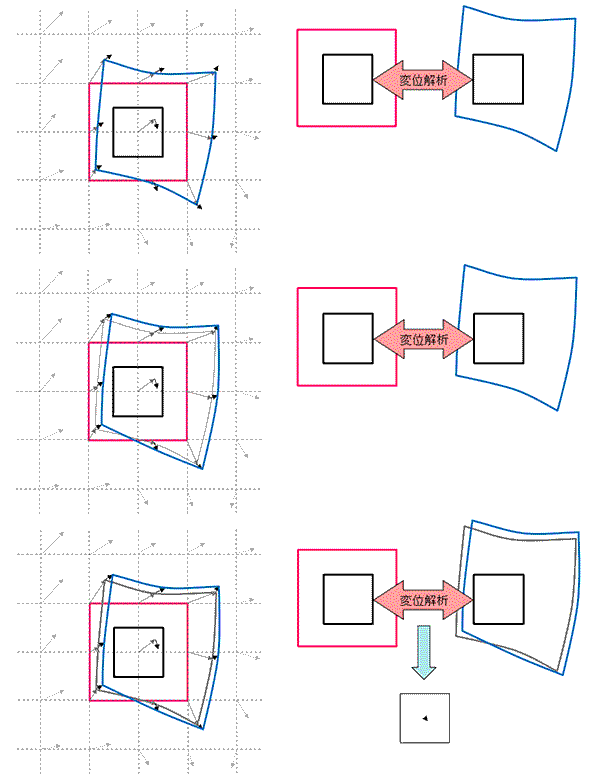
階層相関の概念図です。再帰相関で解析を繰り返す毎にウィンドウサイズを小さくする。最大移動量を大きく保ち、ウィンドウを小さくできるので、速度ダイナミックレンジを保ちつつ空間分解能が向上する。またイニシャルウィンドウ内に回転があっても対応可能。
←横スクロールでご覧いただけます→
 |
 |
 |
 |
 |
 |
 |
| STEP1 | STEP2 | STEP3 | STEP4 | STEP5 | STEP6 | STEP7 |
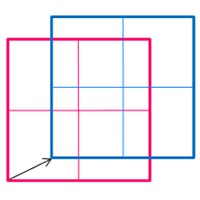
| A画像内のウインドウa(赤枠)とB画像内のウインドウb(青枠)を定義する | ウィンドウa(黒枠)とウィンドウb(青枠)で相関をとり,移動量を求め,次のステップのプレディクター1とする | プレディクター1によりB画像内のウィンドウb(青枠)をシフトし,ウィンドウb’とする | ウィンドウa’とウィンドウb’とも4分割する | それぞれの1/4ウィンドウで相関をとり移動量を求め,プレディクター2(2-1,2-2,2-3,2-4)とする.図はイニシャルウインドウ内に旋回がある場合 | 4つのプレディクター2(2-1,2-2,2-3,2-4)により、B画像内のウインドウB1,b2,b3,b4をそれぞれシフトする | この処理を繰り返すことで精度と分解能を同時に向上が可能.各最終ウィンドウ内の移動先が分割された各グリッドにおける代表移動量になる. |
画像変形 イメージディフォーメーションコリレーション
マルチパスコリレーションやマルチグリッドコリレーションで得られるプレディクターをもとに画像自体を変形させるアルゴリズム。画像変形を再帰的にサブピクセル精度で行うことでピークロッキングによるエラーをほぼ完全に取り去ることが可能。
←横スクロールでご覧いただけます→
時系列PIV専用アルゴリズム FD4
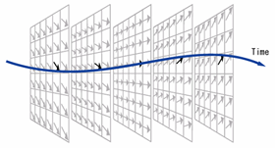
FD4コリレーションは時系列PIVのために開発されたアルゴリズムで、PIVの各グリッドにおける時間的速度変動周波数や乱れの解析、高精度の時空間バリデーション等が可能です。一見、正しそうに見えるベクトル図でも時間軸に沿って解析すると過誤ベクトルが判明する場合があります。
従来の2次元平面内のPIV解析では、解析時に発生した過誤ベクトルは空間バリデーションによって正誤を判断し削除、周囲ベクトル情報からの内挿により補間します。内挿を正しく行うには周囲のベクトルが正しくなければなりません。グリッド上に過誤ベクトルが連続して発生しているようなケースでは内挿が正しく行われないことがあります。
流れは時間的に連続しているので、時系列PIVでは、このような場合にも時間軸に沿った解析により精度の向上が可能になります。
FD4コリレーションの効果
動画の上下のベクトル図は同時刻の瞬時速度ベクトル図です。
両方ともこれだけをみると精度よく解析されているように見えますが、時系列ムービーでみるとFD4コリレーション未適用(上)では渦近傍のベクトルが不自然に振動していることがわかります。
一方FD4コリレーションを適用した(下)データでは各時刻のベクトルが時間的に連続しているのがわかります。
時間軸に沿った解析
時系列PIVでは前後のデータには連続性があるため、過誤ベクトルは空間バリデーションで処理した後さらに時間的に前後のデータと比較して正誤を判断することができます。しかし、時間的に近接しているがゆえに前後のデータも過誤ベクトルになっていることが多いので、前後のデータと比較するだけでは不十分です。
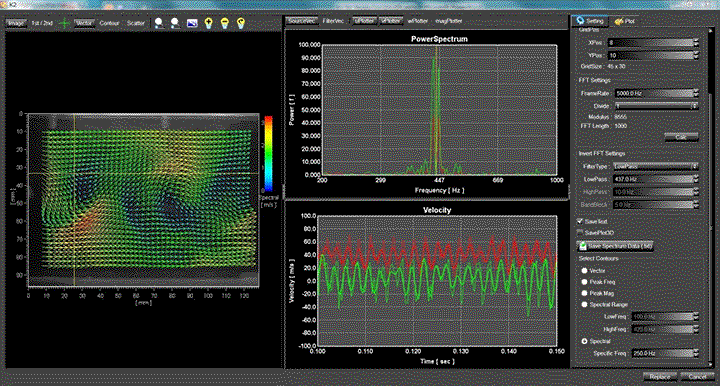
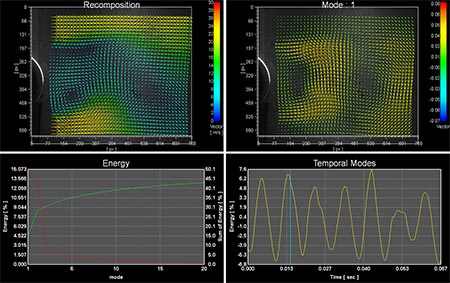
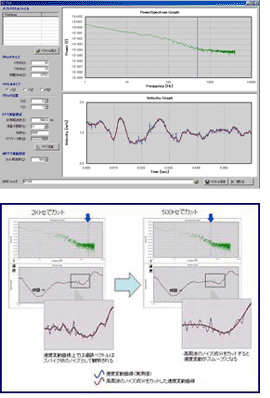
そこでFD4コリレーションはベクトルマップ上の各グリッドにおける時間方向の速度変動のスペクトル解析を行い、当該時刻における理論的最適値を計算します。フーリエ変換により得られた速度変動スペクトルは一般に高周波側はノイズ成分ですので、これに低域フィルターを施し、ノイズ成分を除去した上で、逆フーリエ変換によりタイムドメインデータに戻します。縦軸に速度、横軸に時間をとった速度変動曲線をみると、過誤ベクトルは曲線上にスパイク状のノイズとして観察されます。低域フィルターを施した速度変動曲線はスパイクノイズが消えスムーズな曲線になります。この曲線をもとに当該時刻における理論的最適値を算出することでより信頼性の高い補間値を得ることができます。
FD4コリレーションはこのように空間的な連続性のみを利用した従来方式のバリデーションに加えて時間的連続性も利用することでより高精度の計測を実現します。
※1 時系列PIV用FD4コリレーションは、東京工業大学 宮内・店橋研究室にて開発されたアルゴリズムで、特許技術となっております。